关于二叉树的定义以及遍历方式

#二叉树
二叉树：任何一个节点的子节点数量不超过2，二叉树的子节点分为左节点和右节点

满二叉树：所有叶子节点都在最后一层，而且节点的总数为Math.pow(2,n)个，其中n是指树的高度

完全二叉树：所有叶子节点都在最后一层或者倒数第二层，且最后一层的叶子节点在左边连续，倒数第二层的叶子节点在右边连续
完全二叉树是可以从左向右一直数下去的，如果出现了数数过程中的不连续，那么就说明不是一棵完全二叉树（如果图中没有6和7,那么就不是一棵完全二叉）

##树的遍历
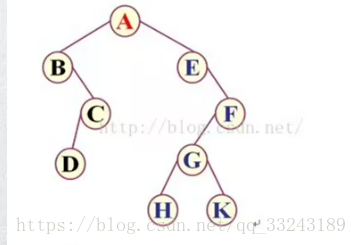
对于下图的二叉树进行遍历时，其三种遍历顺序结果为

前序遍历：ABCDEFGHK

中序遍历：BDCAEHGKF

后序遍历：DCBHKGFEA

前序遍历： 中左右
进行遍历时，先从最中间的根节点开始，然后是左子树，左子树的遍历也是按照先中间，再左边，然后右边的顺序进行的，遍历完左子树，再进行右子树的遍历。先从最中间开始，A，然后再到左子树AB,B没有左节点，故ABC,C结束后再C的先左右节点，ABCD,然后到了A的右子树，查找顺序是一样的，就不再进行赘述了得到ABCDEFGHK

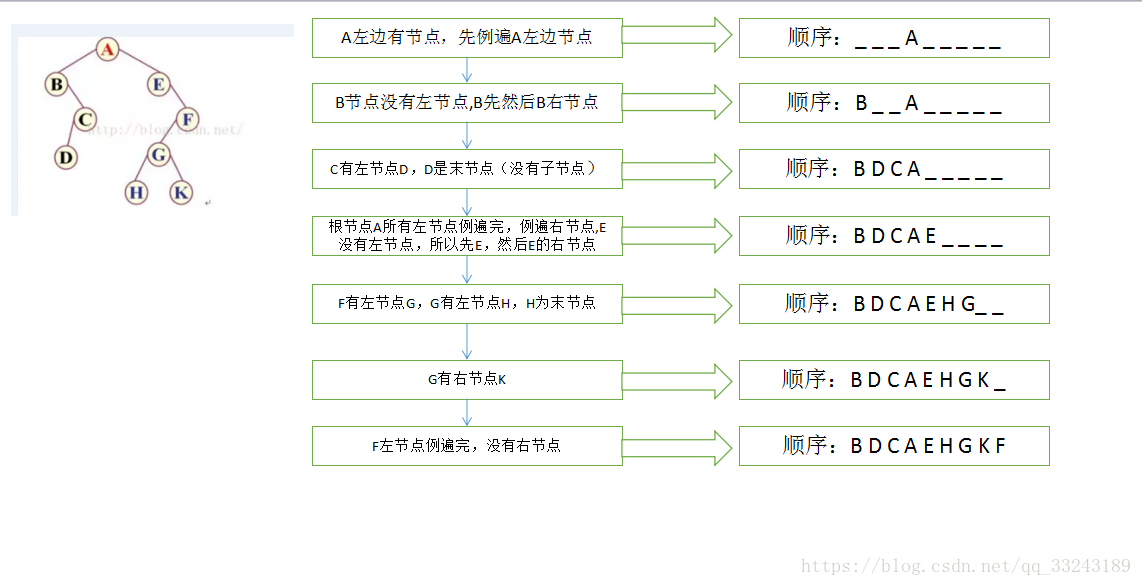
中序遍历： 左中右
先从根节点开始，根节点有左节点，所以到了B位置，然后再找B的左节点的，但是为空，所以第一个为B，再到B的右节点C，此时C有左节点，优先左节点D，然后再C，C没有右节点，这个时候左子树就结束了为BDC,然乎是中间的根节点A，为BDCA，再到右子树，右子树的查找顺序是一样的，先找有没有左节点，然后再中间节点，再右节点，最后得到的结果为:BDCAEHGKF

后序遍历： 左右中
进行遍历时，先从左子树开始，从左子树的左边的叶子节点开始，然后一直到左子树遍历结束，然后右子树，遍历方式是一样的，再是中间的根节点。